What will you learn?
Ask any machine learning expert! They will all have to google the answer to this question:
“What was the derivative of the Softmax function w.r.t (with respect to) its input again?”
The reason behind this forgetfulness is that Softmax(z) is a tricky function, and people tend to forget the process of taking its derivative w.r.t its input, . We need to know this derivative in order to train an Artificial Neural Network. By the end of this post you will have learned the mechanism and the steps required to compute this tricky derivative!
What is a Softmax Unit?
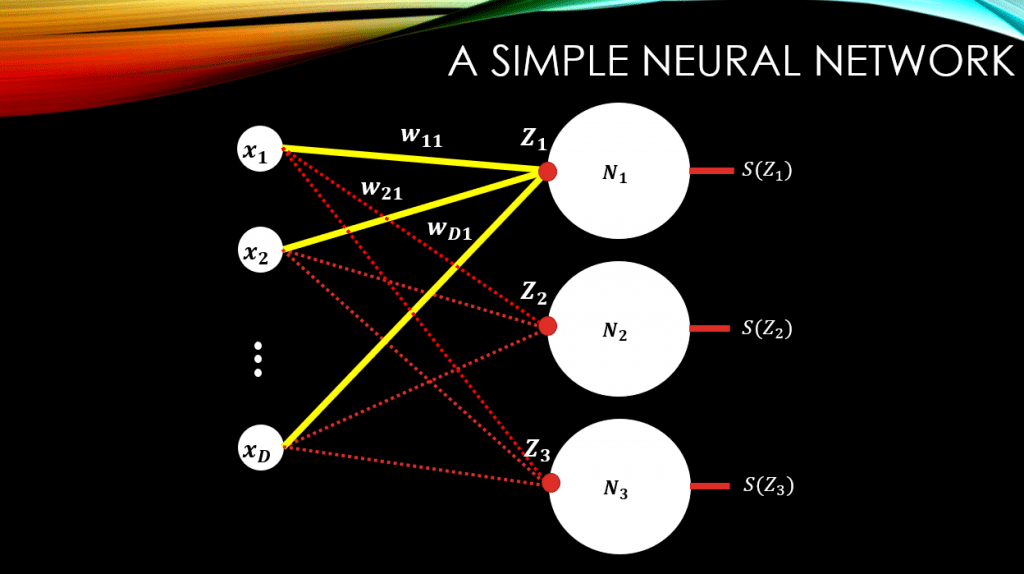
Let’s consider a simple neural network, down below. So we have D-dimensional input data, and some fully connected connections with weights, and our 1 and only output layer. This output layer has only 3 neurons. These neurons, manipulate their inputs using the Softmax function,
, and spit out the result, that is
,
, and
.
Now, let’s remind ourselves as to what the Softmax function really is. In general for an arbitrary vector of inputs, the Softmax function, S, returns a vector
, and the
element of this output vector is computed as follows:
And let us remember that the sum of all ‘s, for all
‘s is equal to 1:
That is the beauty of the Softmax function, as its outputs could be treated as probabilities in a neural network.
NOTE: They are NOT probabilities! But can be treated as a measurement for certainty in a Neural Network.
All of this, is beautifully shown down below:
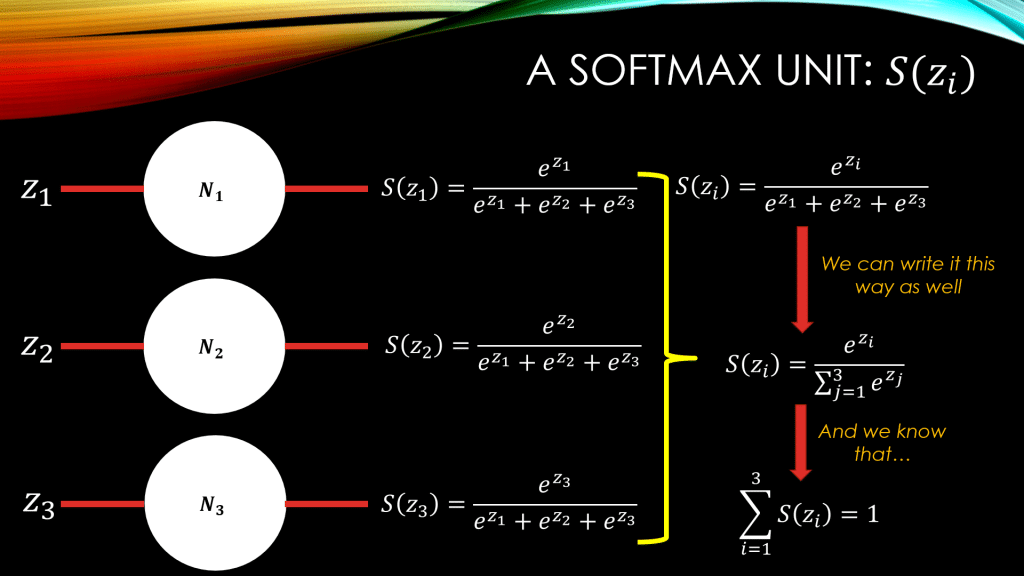
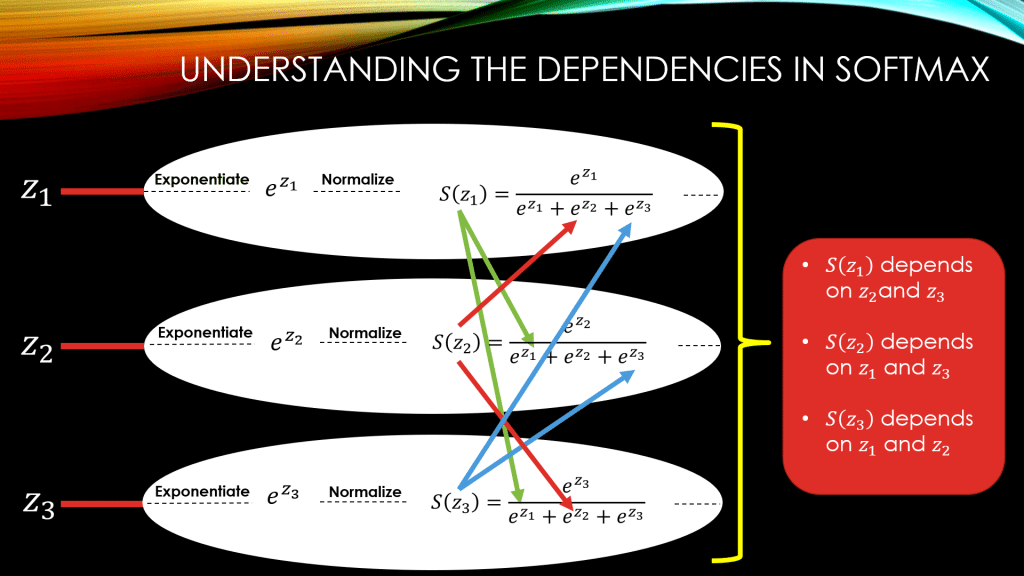
What Makes the Derivative of Softmax Tricky!
The main confusion with this function is the dependencies between the elements of its input vector . So, for example, for computing
, you will need
, and
as well. This is the case, because of the common denominator among all
‘s, that is,
. If you look below, you will see these dependencies beautifully shown with colorful arrows!
So, for example, if you needed to compute the derivative of with respect to just
, since you have used
for computing all
,
, and
, you will need to compute the derivative of all
,
, and
w.r.t
(NOT just the derivative of
w.r.t
).
Below, I have elongated the neurons in our simple neural network, and demonstrated the mathematical operations in each and every one of them. You can see the dependencies by tracing the colored arrows down below:
Computing Each of these Derivatives Separately
Before digging into the math, you need to get comfortable with a few basic mathematical principles of taking derivatives:
Rule#1: The law of independence
Rule#2: The derivative of Exponentials
Rule#3: The derivative of fractions
Rule#4: The derivative of a sum is the sum of derivatives
Knowing what we know now, we should be totally fine with the fact that if we wanted to find the derivative of the softmax function w.r.t any , we would need to consider all of our
‘s, namely in our small example, all
,
, and
.
Let’s start with . Down below, when computing
we are basically considering the first neuron in our neural network, and take the derivative of its output,
, w.r.t its input,
. Take a look at the steps down below:
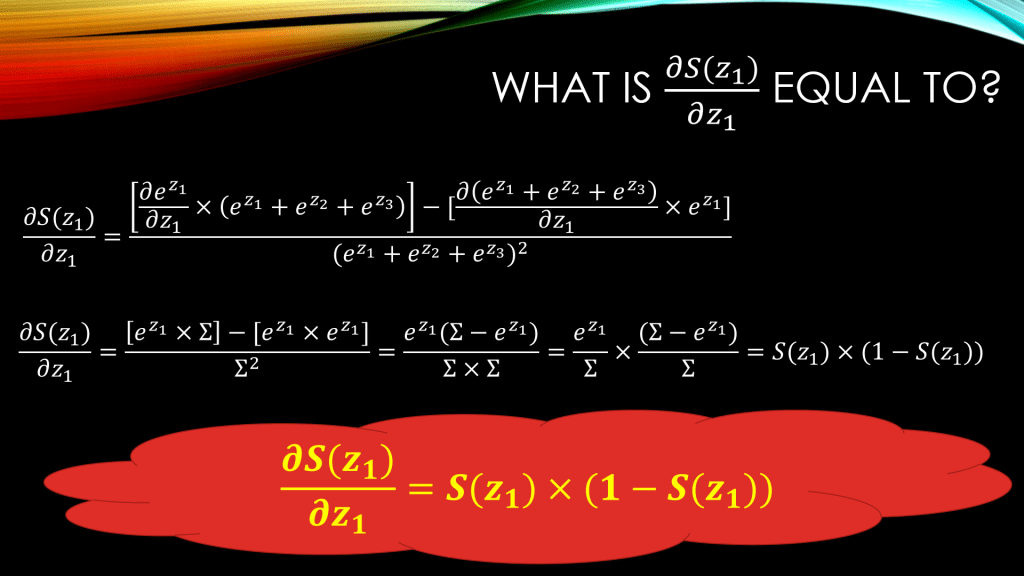
So the first line uses rule number 3 from our derivative rules of fractions. And then in the second line, we can see how as we are using rule number 2 . We are also using rule number 4, as the derivative of a sum is the sum of derivatives, meaning:
And we can immediately use rule number 1 of independence, and conclude that in the equation above, only the first term survives and the second and the third term will become 0!
In the end, in yellow, you can see that when computing the derivative of the output of a Softmax neuron, , w.r.t its direct input
, all we need to do is to
, which is neat and great!
Now, what about ? We need to compute its derivative w.r.t
as well, right? See how beautifully this works out, down below:
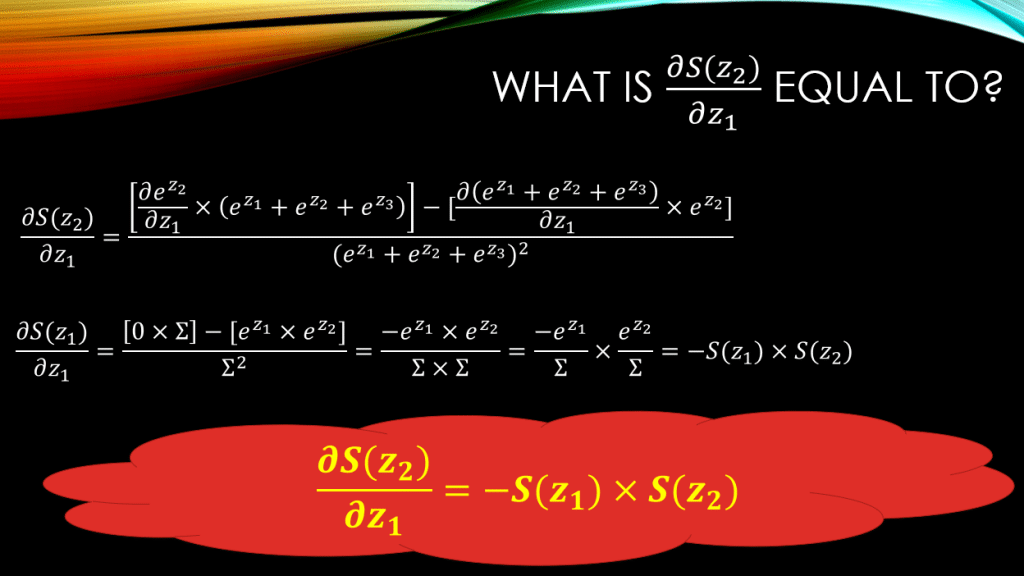
You can see that unlike the case with , now the final result is:
. Can you guess what the result would look like for
? See down below:
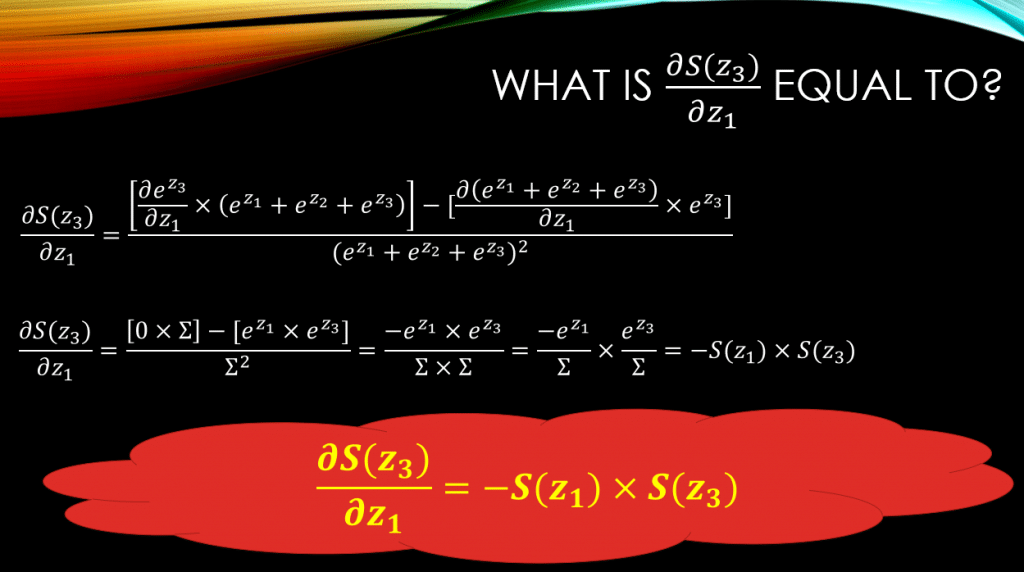
Wow! Just like , again the final result for the partial derivative of
w.r.t
is
.
Can you see the emerging pattern yet? 🙂
So, is there a MAIN Derivative Rule?
So, it all boils down to the index of , and
! Meaning if we are computing
the rule is always:
However, if we are computing , where we are taking the derivative of the output of neuron
, that is
, w.r.t the input of neuron
, that is
. In this case the rule changes to:
. Below you can see all of this, beautifully and mathematically demonstrated:
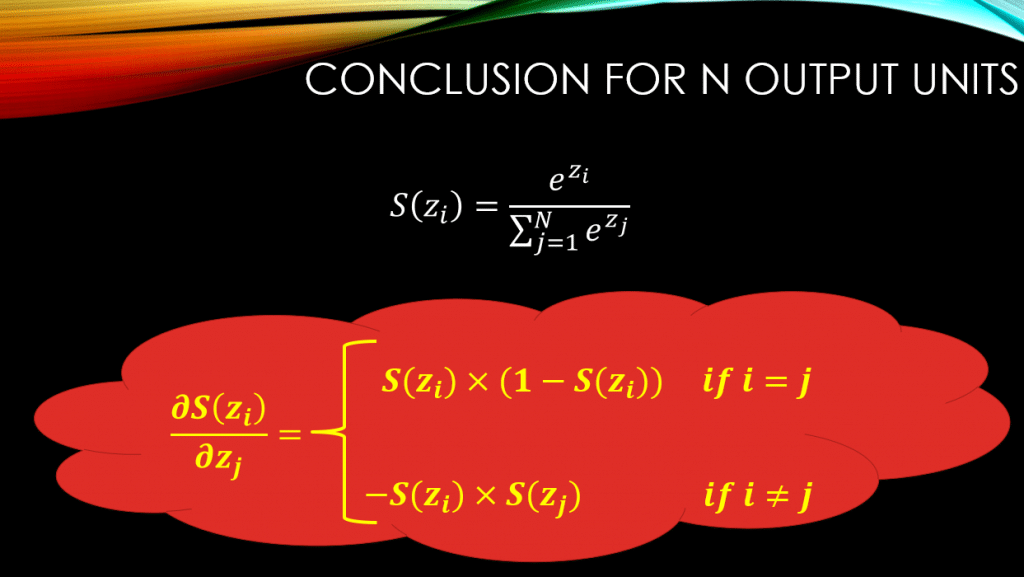
Conclusions
Today, you have learned the basics regarding the famous Softmax function, that is commonly used in Artificial Neural Networks for the task of classification. You have learned about the dependencies between the elements inside the Softmax function and seen how this could make computing the gradient, a little bit tricky. I do hope that this has been helpful.
Until then,
On behalf of MLDawn,
Take care 😉
Author: Mehran
Dr. Mehran H. Bazargani is a researcher and educator specialising in machine learning and computational neuroscience. He earned his Ph.D. from University College Dublin, where his research centered on semi-supervised anomaly detection through the application of One-Class Radial Basis Function (RBF) Networks. His academic foundation was laid with a Bachelor of Science degree in Information Technology, followed by a Master of Science in Computer Engineering from Eastern Mediterranean University, where he focused on molecular communication facilitated by relay nodes in nano wireless sensor networks. Dr. Bazargani’s research interests are situated at the intersection of artificial intelligence and neuroscience, with an emphasis on developing brain-inspired artificial neural networks grounded in the Free Energy Principle. His work aims to model human cognition, including perception, decision-making, and planning, by integrating advanced concepts such as predictive coding and active inference. As a NeuroInsight Marie Skłodowska-Curie Fellow, Dr. Bazargani is currently investigating the mechanisms underlying hallucinations, conceptualising them as instances of false inference about the environment. His research seeks to address this phenomenon in neuropsychiatric disorders by employing brain-inspired AI models, notably predictive coding (PC) networks, to simulate hallucinatory experiences in human perception.






Responses
[…] our previous post, we talked about the derivative of the softmax function with respect to its input. We indeed […]
Hi. Thank you for this. I now truly understand the softmax derivation.
I have a question. Say the error of output S(Z1) w.r.t z1 is A. That of S(Z1) wrt to Z2 is B, and that of S(Z1) wrt to Z3 is C.
So, what is the total error of the output S(Z1)? Do you add A, B, C or multiply them?
Thanks a lot. I am not sure what ‘ the error of output S(Z1) w.r.t z1 is A’ really means! Did you mean the derivative instead of error, perhaps?
Yes, That’s what he meant, and I’m still curious for the answer, is there a summation of derivatives?
Unfortunately I am not sure if I follow. Just work it out manually! The answer should emerge pretty quickly.
I was curious about this too! It seems like a summation as described in this video https://youtu.be/znqbtL0fRA0?si=yOrHkZWy6WUJnWd8&t=2530