Reconciling modern machine learning practice and the bias-variance trade-off

What is This post about?

The interview with the lead author of the paper: Prof. Mikhail Belkin

Together we will analyze an amazing paper entitled: “Reconciling modern machine learning practice and the bias-variance trade-off “. You know how we always thought we understood how increasing model capacity (e.g., increasing the number of parameters in an Artificial Neural Network) after a certain point, can lead to over-fitting? We always needed to find the sweet spot, if you will, where the model capacity is just enough to fit the training data and to generalize well to the unseen data. Below is the famous U-shape figure:

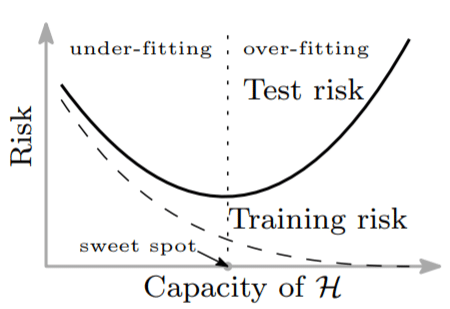
You can see how after the sweet spot, the training risk (aka., training error) still goes down, while the test risk (aka., test error) keeps increasing. Thus, capacities before the sweet spot, at the sweet spot, and after the sweet spot, result in under-fitting, good-fitting, and over-fitting (Or so we thought!!!). The paper we analyze today, shows us that if we ignore the disturbing increase in the test risk, and keep increasing the model capacity, there will come a 2^nd descent where we might even achieve a better generalization than if we had used the model capacity at the “sweet spot”: This is the Double Descent behavior!

I am ready when you are 😉

The Double-Descent Risk Curve

If we increase the capacity of a model beyond the sweet spot, we enter the realm of over-fitting and if we just ignore this and just keep adding more parameters, we will hit a spot where the model fits the training data perfectly. Let’s call this the interpolation point. This is where the generalization ability of our model is at its worst, that is, the test risk is maximum! Amazingly, the authors did not give up and kept increasing the model capacity beyond this point and that is where an amazing phenomenon happens! The test risk starts dropping again (i.e., the model’s generalizability begins to improve) and the more parameters you add it will become better and better. This is where the second descent in the previously-known balance-variance trade-off curve happens! You might wonder so what? Here is what:

The authors have shown that if you keep adding parameters to the model beyond the interpolation point, there will be a second descent that could even lead to a generalizability that is higher than what you would achieve if you stopped at the sweet spot in the classic U-shape curve.

One important issue to remind ourselves of is the following: It is not always true that the second descent has better generalization than the bottom of the traditional U-shape curve. In simulations it can go either way depending on the specific parameters. In practice it is hard to tell for sure, but presumably, this also depends on the specific settings.

Who would have thought, all these years, we had been seeing only half of the bigger picture! Let’s see the astonishing double-descent curve:

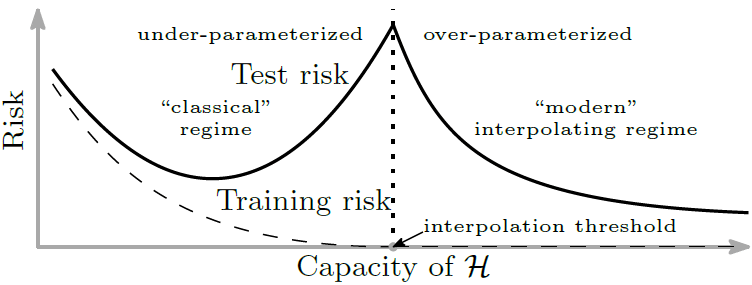
Very interestingly, the double-descent phenomenon can explain why models with millions of parameters, say monstrous Artificial Neural Networks, can still accomplish a low test risk! This is amazing, as the previously known U-shape curve could not justify why these big models can still achieve such good generalizability! This explains why very rich deep neural networks tend to perform so well and generalize so beautifully. Such models (in modern interpolating regime) are over-parametrized beyond the interpolation point as opposed to the classical regime (i.e., any model with capacities below the interpolation threshold).

The authors highlight a very interesting insight:

Models with high capacity can achieve low test risk (i.e., high generalizability) because the capacity of the model does not necessarily reflect how well the model matches the inductive-bias appropriate for the problem at hand!

For the datasets used in the paper the authors argue that smoothness or regularity of a function is the appropriate inductive bias, which can be measured by a certain function space norm. In particular in such problems, modern monstrous deep learning architectures find low norm solutions, which implies smooth functions without mad oscillations. It is very interesting to note that choosing the smoothest function that fits the training data perfectly reminds us of Occam’s razor that states that:

Simplest explanation compatible with the observations should be preferred!

By considering models with high capacity, in a way, we are considering a larger set of candidate functions that not only fit the training data perfectly but also have smaller norm and thus are “simpler”. This is how the authors believe high-capacity models can improve the performance (i.e., generalizability) dramatically! For understanding functional norms, you can take a look at the theory of Reproducing Kernel Hilbert Spaces (RKHS) or the related theory of Sobolev spaces. These norms are similar to vector norms in their properties but they control the smoothness of the function.

Double-Descent in Practice and Empirical Proof

Let’s see the empirical results that are reported in the paper, where we can see how the double descent happens in practice.

Neural Networks: Artificial neural networks have been investigated and applied to the famous MNIST dataset and the test risk is computed as opposed to the capacity of the neural network. In particular, they have used a single layer fully-connected neural network with $H$ hidden units, where the number of parameters (i.e., weights) are used to increase the capacity of the model. This is a classification task, and the job is to learn to classify hand-written digits into their corresponding correct classes, of which we have 10, one for each digit: 0,1,2,…,9. In this case, the number of data samples are $n=4 \times 10^3$ , the dimensionality of the data, $d$ , is 784 (remember: the images in MNIST are 28×28 pixel which amounts to 784 pixel values), and the number of classes, $K$ , is 10. The number of parameters is then $(d+1)\times H+(H+1) \times K$ . The reason for adding 1 in this formula is that in both the input layer and the hidden layer there is an additional bias unit. The interpolation threshold (black dotted line) is observed at $n \times K$ .

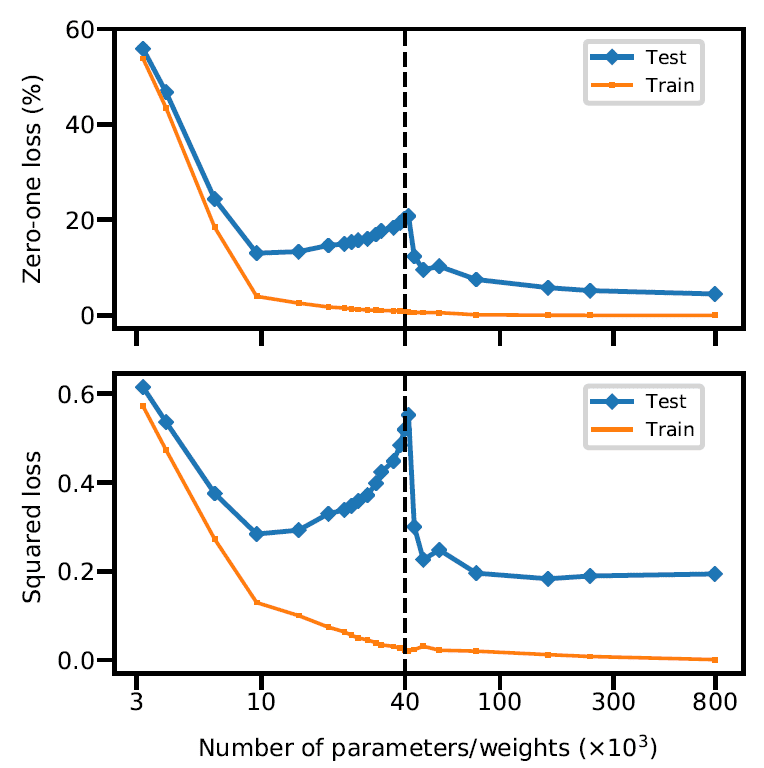
It is absolutely astonishing that we can see how the double-descent is happening right before our very eyes! This happens whether a simple Zero-loss or the squared loss is used!

However, what structural mechanisms, as the authors put it, account for the double descent shape?

This has something to do with the number of features, $N$ and the number of data instance, $n$ . When the number of features is much smaller than the number of data instances (i.e., $N << n$ ), the training and test risks are close. This is where by adding more features (i.e., increasing $N$ ) the performance on both train and test sets will improve. However, as the number of features approach the number of data instances (this is the interpolation point $N=10^4$ ), the test risk is at its peak which means we are maximally over-fitting! This is where, we have increased the number of features to a point where some features that are not present in the data (or even weakly present) are forced to fit the training data almost perfectly. However, the authors kept on pushing and increased the number of features beyond the interpolation point! By increasing the number of features, a better and better approximations to that smallest norm function (i.e., the simplest and smoothest function) can be constructed.

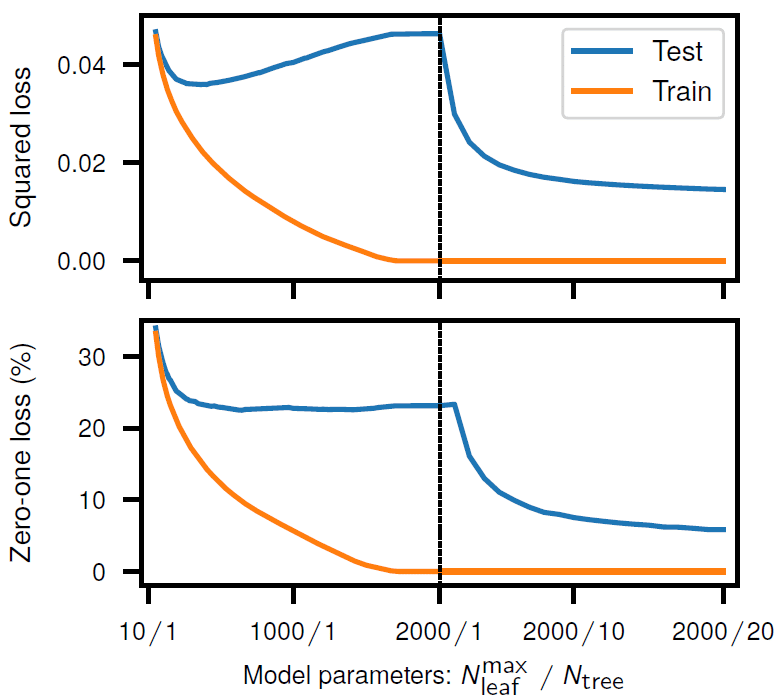
Random Forests: The same experiment as before is done, however, using a random forest model this time. The double descent risk curve is observed for random forests with increasing model complexity trained on MNIST ( $n$ = 104; 10 classes). Its complexity is controlled by the number of trees $N_{tree}$ and the maximum number of leaves allowed for each tree $N_{max}$ .

Conclusion

It is astonishing how a principle, such as the U-curve of the bias-variance trade-off can be challenged and re-learned! This paper shows us why on earth the modern machine learning models, with such high capacities, do not over-fit and generalize so strongly to the unseen test data. Indeed, all these years, we have been looking at ONLY a part of the big picture, the single descent, whereas the has always been a bigger picture, that is, the double-descent bias-variance trade-off.

I hope this has been informative and Kudos to the authors of this amazing paper.

On behalf of MLDawn,

Take care of yourselves 😉