Introduction
If we really wanted to simplify the whole story behind “Learning” in machine learning, we could say that a machine learning algorithm strives to learn a general function out of a given limited training examples. In general, we can think of concept learning as a search problem. The learner searches through a space of hypotheses (we will explain what they are), to find the best one. Which one would be the best one? The answer is the one that fits the training examples the best. And while searching and trying different hypotheses, we would hope for the learner to eventually converge to the correct hypothesis. This convergence is the same idea as Learning! Now, let’s go deeper…
What does a Concept mean after all?
A concept means the spirit of something, the category of something. For example, as human beings we have learned the concept of Ship. We know what it is, and no matter how many new, high-tech and fancy ships we are shown, we can still classify them as ships, even though we might not have seen those specific models before! We can do this because we have learned the general concept of ship that encompasses infinite number of different kinds of ships that were, are, or will ever be built! What other concepts can you think of?
Bird
Stressful situation (That is right! A concept doesn’t have to be a physical object)
cold/hot/humid
And so on and so forth. Now please note that, on a more technical level we can think of a concept as a boolean function! As we know, every function has a domain (i.e., the inputs) and a range (i.e., the outputs)! So can you think of the domain and range of a boolean function that represents a concept such as the concept of bird?
hint: Remember that this function is true for birds and false for anything else (tigers, ants, …)
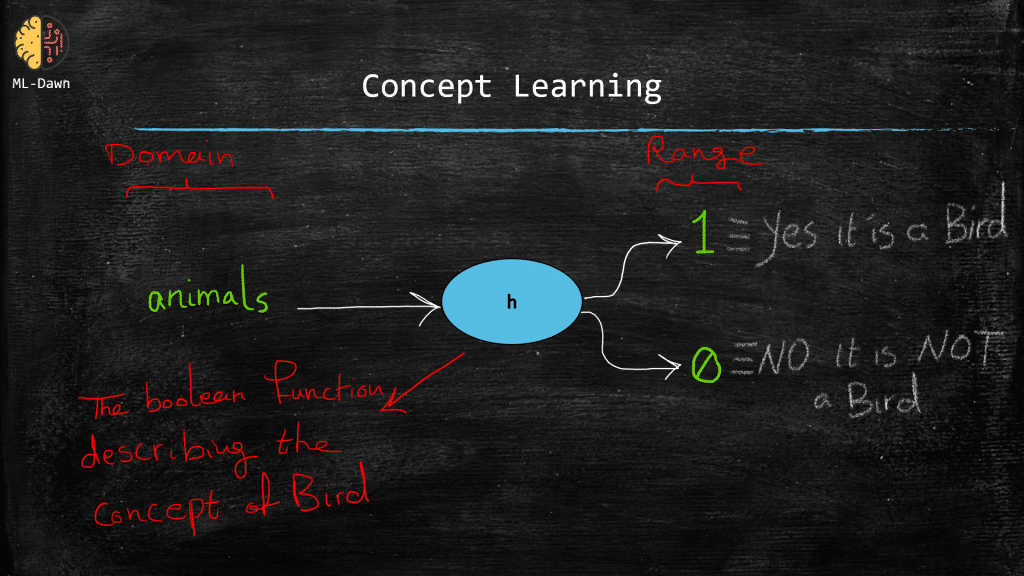
So this explanation makes machine learning more tangible, doesn’t it?
“A machine learning algorithm tries to infer the general definition of some concept, through some training examples that are labeled as members or non-members of that particular concept”
So this is called concept learning and the whole idea is to estimate the true underlying boolean function (i.e., concept), which can successfully fit the training examples perfectly and spit out the right output. This means that if the label for a training example is positive (i.e., a member of the concept) or negative, we would like for our learned function to correctly determine all these cases.
Note: The idea of labels in the training examples implies supervised learning. Please note that we don’t always have labels for our data. In these cases, unsupervised learning, we need to resort to other techniques to understand the training data and extract the concept out of them. Again we are learning a boolean function, but this time, the range of this function is NOT the labels associated with the training examples. You can think of the Auto-Encoders, which are ideal for unsupervised learning, and specifically for one-class classification:(aka. Anomaly Detection). For those of you who are interested, in a standard Auto-encoder, we try to reconstruct the input examples! This might seem crazy but actually if we are able to reconstruct the training examples, then we have learned the behavior/distribution of the training data, but we are not going to go there in this post.
An Example for Concept Learning
Let’s say the task is to learn the following target concept:
Days on which James will play golf
Down below, in the slide entitled “concept learning example“, you can see a set of example days, where each example consists of a set of attributes. Now, please note that the very last attribute, play, also known as the label or the ground-truth, shows whether James plays golf on that specific day.
We mentioned that the machine searches in the hypothesis space, to find the best hypothesis fitting the training examples. The big questions are:
What is a hypothesis?
How do we represent a hypothesis to a machine learning algorithm?
We can simply define a hypothesis as a vector of some constraints on the attributes. In our example below, a hypothesis consists of 3 constraints. Now, a constraint for a given attribute could have different shapes and forms:
Totally free of constraint (denoted with a question mark): This means that we really don’t put any constraint on a particular attribute as that attribute doesn’t play an important role in learning the concept of play in this hypothesis. (Please note that a hypothesis could consists of terrible constraints that will constantly fail to describe the concept. This is why the learner will search in the hypothesis space with the hopes of finding the best hypothesis)
Strong constraint on the value of the attribute: specified by the exact required value for that particular attribute
Strong constraint regardless of the value of the attribute: no value is acceptable for the attribute. Meaning that no day is a positive example (i.e., play=yes). Now, obviously we have examples in our table with “play = yes“, so you can immediately see why a hypothesis with no value acceptable for any of its attributes, is a bad hypothesis in this example!
It is important to remind ourselves that if a given training example x (or a test example for that matter), could satisfy all the constraints in a given hypothesis h, (i.e., h(x) = 1), then we can say that hypothesis h classifies x as a positive example (i.e., play = yes). Otherwise, if x fails to satisfy even one constraint in h, the h(x) = 0, and this means that hypothesis h classifies input x as a negative example (i.e., play = No).
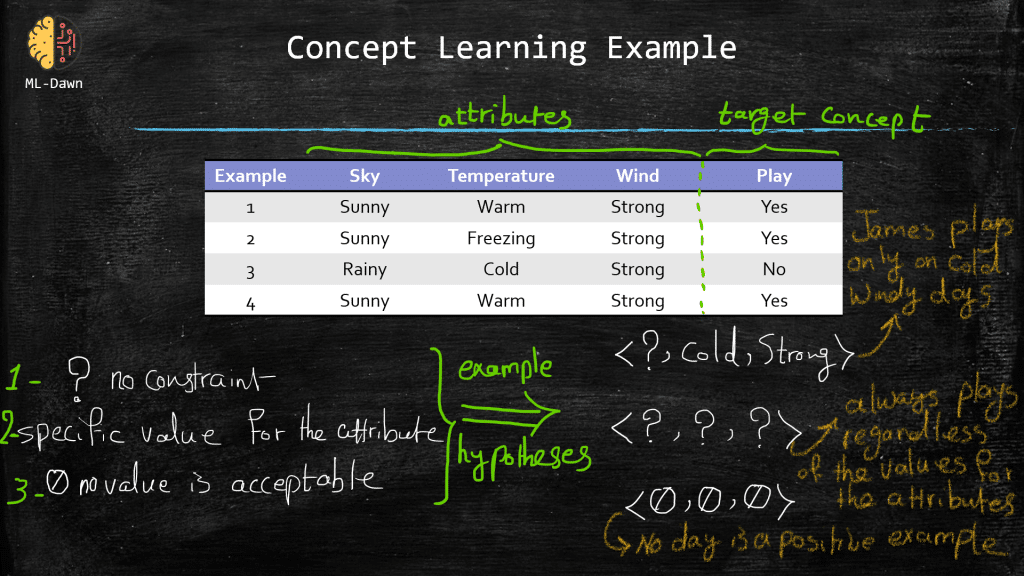
Now while a machine learning algorithm searches in the hypothesis space and tries to fit each one to the training examples, we hope that after the search is done, the learner will have found the true underlying hypothesis C! Basically, you can think of C as what we would like to estimate by trying different hypotheses. C is what we hope to converge to by trying different hypotheses!
So, for a positive training example x, C(x)=1 and for a negative training example C(x) = 0! Remember that we don’t know C but are trying to estimate it! So we can basically describe a training example x and its corresponding label as an ordered pair <x, C(x)>. We can say that the main job of the learner is to hypothesize and find a hypothesis h such that for every training example x in the training set: h(x) = C(x)!
The Inductive Learning Hypothesis
Yes, we look for the best-fit hypothesis that is identical to the true hypothesis C over the whole set of training instances! But of all the instances, we only have access to the available training examples at hand. As a result, ideally, the learned hypothesis will fit C perfectly, but JUST over the training examples! It is because the only knowledge we have about C is its output for the training examples that we have at hand. There will be unseen data for sure and that is where we hope that the learned hypothesis h that has done great on the training examples will do great on the unseen data (i.e., generalizing well)! This seems like an aggressive generalization but that is what happens out there in the machine learning world! The assumption is that during training, the best hypothesis for the future unseen data, is the one that best fits the available training examples where h(x) = C(x) for every x in our training set. This is the fundamental assumption of the inductive learning hypothesis.