A Quick Recap on our Last Post
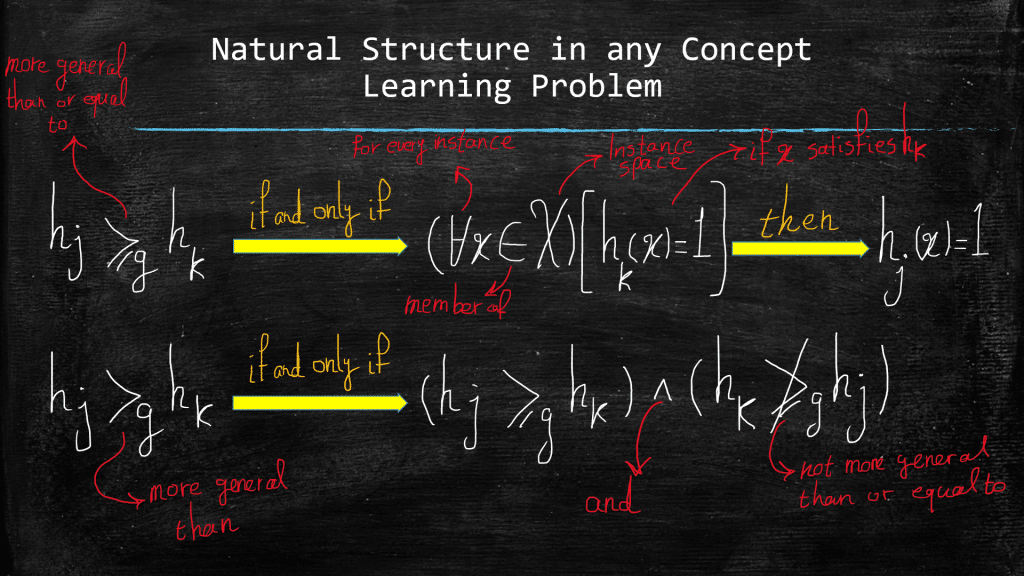
In our last post, we talked about the more-general-than-or-equal-to operation, which we denoted with ≥g and we said that in order for hypothesis hj to be considered more general than or equal to hypothesis hk, the following has to hold:
Today, we will talk about a famous algorithm that can be used to explore the hypothesis space, H, by leveraging the ≥g operation to its advantage. The name of this algorithm is: Finding-S, where S stands for specific, and hints that the goal is to find the most specific hypothesis. Below we dig deeper to understand this interesting, but not perfect, algorithm!
Find-S: Finding the Most Specific Hypothesis
So, how can the more-general-than-or-equal-to operation help us improve our search in the hypothesis space H? The Find-S algorithm suggests that we could start with the most specific hypothesis, and then progressively generalize it every time it fails to correctly classify a positive example in our training set. We do this generalization to ameliorate this failure! Remember that an example x is classified as positive by hypothesis h, if and only if:
h(x) = 1
Below, you can see steps of the Find-S algorithm:
Every algorithm can be explained better through a practical example, yes? First take a look at the table of training examples below:
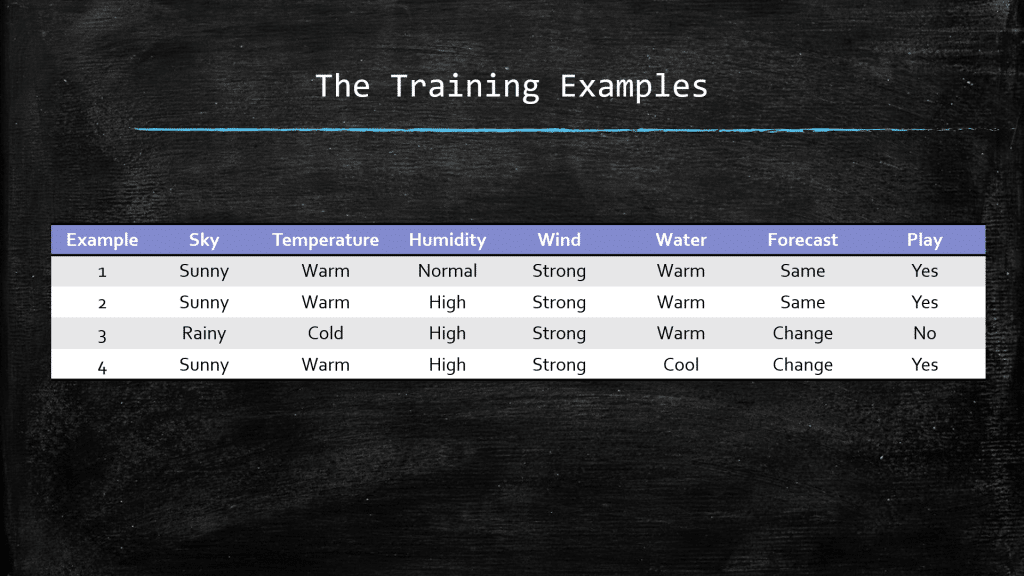
Remember that we want to learn the concept of play so we can understand what is the playing habit of Joe. Meaning in what type of a day would he play golf?! all we have at hand is the limited and yet valuable set of training examples (A small set of the instance space: All possible days!). Let’s follow the algorithm:
- We start by the most specific hypothesis, meaning the most limited and constrained one in H:
h = <Ø,Ø,Ø,Ø,Ø,Ø>
- Now we walk through the training examples. Upon observing the first training example
x1 = (Sunny, Warm, Normal, Strong, Warm, Same)
- which happens to be a positive example (i.e., Play = Yes), we can see that h is too specific to be satisfied by this training example (or for any positive training example for that matter). So the next step is to replace every constrained in h that are not satisfied by x1, with the NEXT more general constraint that could make h satisfiable by this training example. So, NONE of the Ø constraints can be satisfied by this training example, so what is the next more general value for each one of the Ø constraints that could make h, just general enough to have classified x1 as positive? One might suggest: “replace all of the Ø constraints with the question mark constraint ?“. The answer to this BIG step of generalization is that, yes, the new h will definitely classify x1 as positive. But as you can imagine, it classifies literally EVERYTHING else as positive as well! Now this is definitely a catastrophe as h will lose any discriminatory functionality which is needed for building a classifier in the first place. So, we need to generalize h just enough to classify x1 as positive! So, another solution is to literally, replace every Ø constraint with its corresponding attribute value in x1. This makes h satisfiable by x1:
h = <Sunny, Warm, Normal, Strong, Warm, Same>
- Now, this new h is a little bit less specific than the previous h, in that there is at least 1 training example that can satisfy it (i.e., x1). But it is still pretty limited, as it will classify anything else as negative, which is again catastrophic! We need more generalization as we will see in the following.
- Our next training example, which happens to be a positive example again, is:
x2 = (Sunny, Warm, High, Strong, Warm, same)
and we can see that there is only 1 value in x2 that prevents x2 from satisfying our current hypothesis h, and that is the value for the attribute “Humidity”! Our most updated hypothesis h, requires that the “Humidity” level be “Normal” whereas in x2 , it is High. However, all the other attribute values in x2 can satisfy their corresponding constraints in h. So, we need to do something with the current constraints on “Humidity” in h. The constraints on “Humidity” was Ø at first, then we had to change it to “Normal” to adapt to our first observed training example x1. And now, x2 has the value “high” for “Humidity”!
- So, what sort of constraint should we have for “Humidity”, so that it could be satisfied by x2 and yet be satisfied by the first example x1? Yes! The answer is the question mark constraint “?”, which is satisfiable with both “Normal”, and “High”, found in x1, and x2. So the next more general hypothesis is:
h = <Sunny, warm, ?, Strong, Warm, Same>
Upon seeing the third training example, which happens to be a negative example, the Find-S algorithm simply ignores it and makes no change to the currently found hypothesis. However, notice that h is already classifying this negative example x3 as negative (i.e., h(x3) = 0), meaning that x3 fails to satisfy h, so no change on h is needed!
IMPORTANT: Note that at any stage of our search in Find-S algorithm, the obtained hypothesis h, is the most specific hypothesis that is consistent with the observed positive example. Remember that we are seeking the hidden desired hypothesis c in the hypothesis space, and we know that c is definitely, 100%, consistent with the positive training examples, so target hypothesis c (i.e., the target concept) is for sure more-general-than-or-equal-to h. Remember that the target concept c will never cover the negative examples (i.e., negative examples cannot satisfy c), so since we just established that:
c ≥g h
Then those negative examples cannot satisfy h either, as we know that c encompasses h. Finally, upon arrival of the fourth example x4:
x4 = (Sunny, Warm, High, Strong, Cool, Change)
We can see that the last 2 values “Cool” and “Change” fail to satisfy our current h! So, h needs to evolve to the next more general hypothesis that is:
h = <Sunny, Warm, ?, Strong, ?, ?>
Concluding Remarks on Find-S
- Find-S is NOT perfect! It just shows one way to leverage the more-general-than-or-equal-to relationship to have a more guided progressive search from hypothesis to hypothesis in H. We will talk about the issues with this algorithm in the next post!
- Remember that we are assuming that H indeed contains the true hypothesis c that describes the concept we would like to learn, perfectly! And also we are assuming that the training examples are error-free! Find-S can result in bad hypotheses if say it generalized h to cover an example which is mistakenly labeled as positive (i.e., noise in the training examples).
- At each step, the hypothesis is generalized just as much to cover the current observed positive example! Not more! We are taking small steps to avoid over-generalizing our hypothesis!
- At any step, the obtained hypothesis h, is the most specific hypothesis in H that is consistent with the observed positive training examples up to that point.
- Note that the way we generalized the constraints in h went like this:
Ø –> a specific value –> ?
So, we mean that the next general constraint after Ø is a specific value, and after that we resort to ? which says anything goes. Note that the jump from a specific value to ? is quite aggressive and makes a huge generalization but then again these 3 constraint types are just there to smooth out the bits and pieces and implementation of the Find-S algorithm. The Find-S algorithm has nothing to do with our defined constraints and these constraints have been defined just to convey the big picture about meaning of a more general / more specific hypothesis, and that’s all.
In the next post we will focus a little bit more on this algorithm and talk about some of the issues with it.
Until then, take care! (ML-Dawn)