Hello friends and welcome to MLDawn!
So what sometimes concerns me is the fact that magnificent packages such as PyTorch (indeed amazing), TensorFlow (indeed a nightmare), and Keras (indeed great), have prevented machine learning enthusiasts to really learn the science behind how the machine learns. To be more accurate, there is nothing wrong with having these packages but I suppose we, as humans, have always wanted to learn the fast and easy way! I am arguing that while we enjoy the speed and ease of coding that such packages bless us with, we need to know what is happening behind the scene!
For example, when we want to build a complicated multi-class classifier with a sophisticated Artificial Neural Network (ANN) architecture, full of convolutional layers and recurrent units, we need to ask ourselves:
Do I know the logic behind this?! Why convolutional layers? Why recurrent layers? Why do I use a softmax() function as the output function? And why do people always use cross-entropy as the appropriate error function in such scenarios? Is there a reason why cross-entropy pairs well with softmax?
So, one way we could understand the answer to some of these questions, is to see whether we can implement a simple binary classifier on some synthetic 1-dimensional data using the simplest ANN possible, from scratch!
In this post we will code this simple neural network from scratch using numpy! We will also use matplotlib for some nice visualisations.
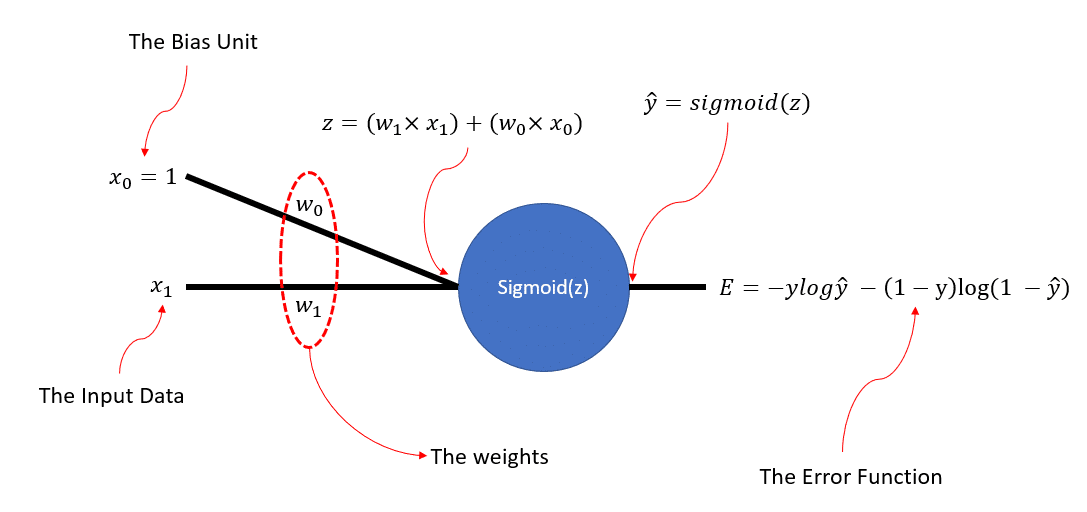
So, if we consider our synthetic data to be a bunch of scalars, and 1-Dimensional, this is the simple ANN structure that we could be interested in building from scratch!
Right! So, now it is time to do the coding bit. First foremost, let’s import the necessary packages! The almighty numpy and matplotlib’s pyplot are both needed.
|
1 2 3 4 |
# Import numpy for all mathematical operations and also generating our synthetic data import numpy as np # Matplotlib is going to be used for visualisations import matplotlib.pyplot as plt |
I am sure that as a Neural Network enthusiasts, you are familiar with the idea of the sigmoid() function and the binary-cross entropy function. We need to use them during the forward-pass. Before showing you the code, let me refresh your memory on the math: %20%3D%20%5Cfrac%7B1%7D%7B1%20%2B%20e%5E%7B-z%7D%7D)
and as for the binary-cross entropy:
Note that: The base of the logarithm is e. Meaning that what we have here is the Natural Logarithm!
Remember that this error function is nothing but a measure of difference between the output of the ANN, 
, and the ground-truth, y. So, the lower the better!
Now let’s see the code. We can code both of these 2 functions using 2 separate python functions:
|
1 2 3 4 5 6 7 8 9 |
def Cross_Entropy(y_hat, y): # Note that y could be either 1 or 0. If y=1, only the first term in the Error survives! And if y=0, only the second term survives! if y == 1: return -np.log(y_hat) else: return -np.log(1 - y_hat) def sigmoid(z): return 1 / (1 + np.exp(-z)) |
Now, we have to think ahead, right? So, during the back-propagation phase, we will need 2 things!
-
The derivative of the Error w.r.t the output
-
The derivative of the output
Now, as a reminder:
And as for the sigmoid(z), or for short, sig(z):
This is not a neural network course, so I am not going to derive these here mathematically. Now, let us see the 2 functions in python, whose job is to compute these derivatives:
|
1 2 3 4 5 6 7 8 |
def derivative_Cross_Entropy(y_hat, y): if y == 1: return -1/y_hat else: return 1 / (1 - y_hat) def derivative_sigmoid(x): return x*(1-x) |
Next, we need to generate our data points. We could use 2 random normal distributions to generate our 1-Dimensional data points. We will make sure that they are somewhat linearly separable, for simplicity. We can control these distributions by tweaking the parameters of these 2 Gaussians. For example, in our code below, we have made sure that the mean (i.e., the center) of the second Gaussian is 5 units away from the first Gaussian, whose mean is 0. Also, we have made sure that the standard deviation of the second Gaussian is half of the first Gaussian, whose standard deviation is 1. By randomly generating 500 samples from the First Gaussian and 500 samples from the second Gaussian, we have generated the data for class 0 and class 1 in our newly born dataset. Below you can see the code for doing this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# Define some artificial data area = 200 # The number of samples for each of our 2 classes N = 500 # The reference mean and standard deviation for generating 500 samples for one of the classes mu, sigma = 0, 1 # Here we sample 500 samples from our first Gaussian for class 0 x_0 = np.random.normal(mu, sigma, N) # Here we sample 500 samples from our first Gaussian for class 1. Note how we are tweaking the # means and standard deviation with respect to the first Gaussian x_1 = np.random.normal(mu + 5, sigma*0.50, N) # A scatter plot for plotting samples of both classes with area = 200. The y value for all the points is 0 (i.e., they are 1-Dimensional datapoints) plt.scatter(x_0, np.zeros_like(x_0), s=area, c='r', alpha=0.5, label="Class 0") plt.scatter(x_1, np.zeros_like(x_1), s=area, c='c', alpha=0.5, label="Class 1") # This line makes the labels of the plot, actually appear as legends on the plot plt.legend() # Let's put some limit on the vertical axis (Remember that our data points have NO second dimension) So, plt.ylim(-0.2, 1.25) # Put some grid on the plot plt.grid() # Show the bloody plot ;-) plt.show() |
And here you can see the our generated data from both Gaussians:
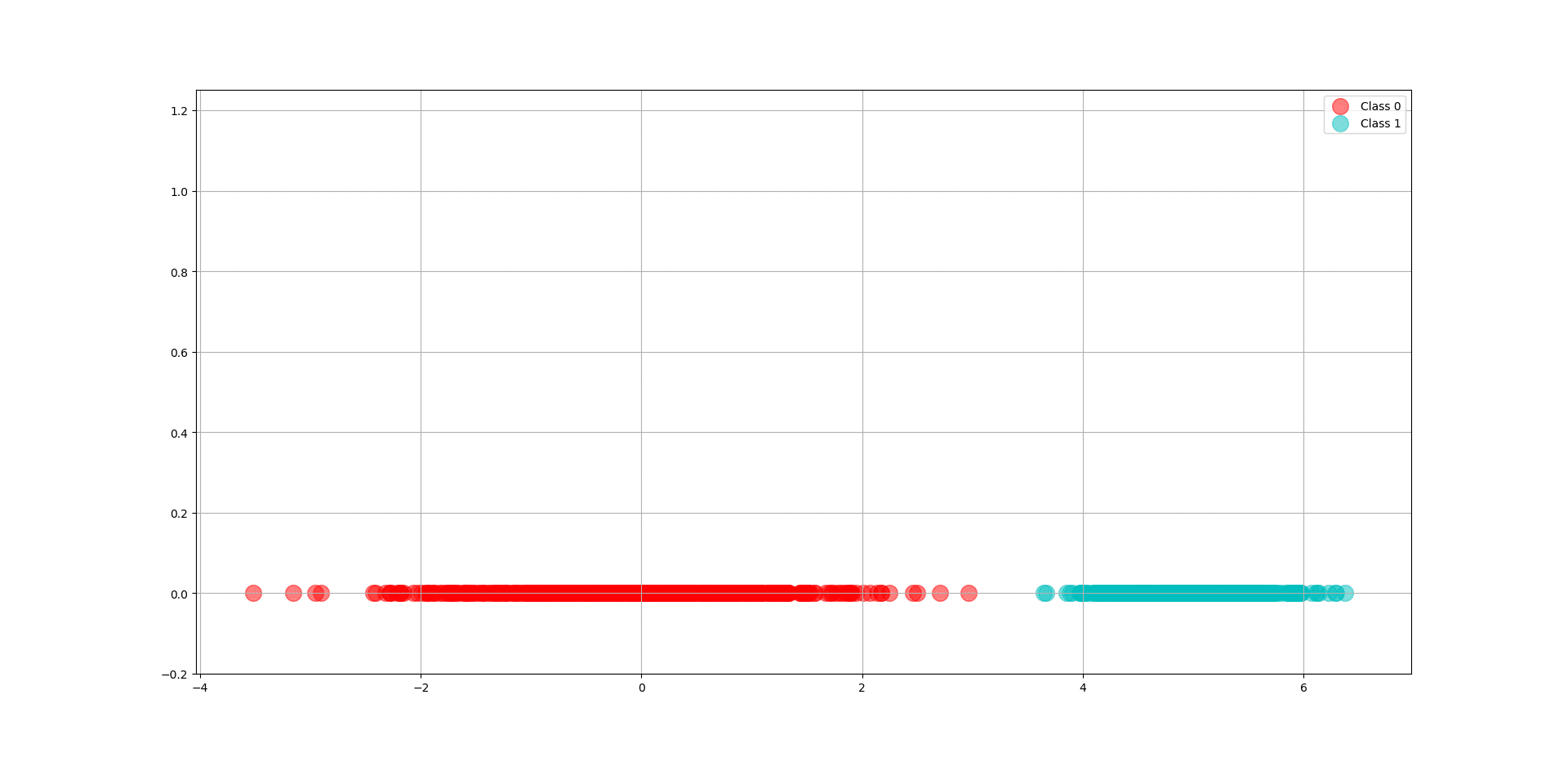
So now we have these data points as our training data. However, remember that our binary classifier is a supervised algorithm and just like any other supervised machine learning algorithm we need the ground truth for our training data. More specifically, since we have 2 classes, we would consider 500 zero’s for the data points belonging to class 0, and 500 one’s for the data points belonging to class 1.
You must remember that, for a binary classification problem, we tend to use the sigmoid() output function. A sigmoid() generates values between 0 and 1, and we would like to learn the weights in our ANN in such a way that the generated sigmoid() function, would output 1 for all the instances in class 1, and 0 for all the instances in class 0.
So, the code below, concatenates all the data points in 1 big numpy array, X, that is the entire training set. And then we generate the ground truth (i.e., the labels), namely, 500 zeros’s and 500 one’s as one big ground truth numpy array, called, Y.
|
1 2 3 4 5 6 7 8 9 10 11 |
# Define X, Y as data and labels. Now X has 1000 values. X is now a list X = [x_0, x_1] # Create the ground truth numpy array. np.zeros_like(x_0) generates a numpy array full of # zeros with the same dimensions of x_0 now Y has 1000 elements inside of it Y = [np.zeros_like(x_0), np.ones_like(x_1)] # Both X and Y are now lists and NOT numpy arrays. Let's convert them X = np.array(X) Y = np.array(Y) # Now the dimensions of both X and Y is (2, 500). Let's make it 1000 (i.e., flattening) X = X.reshape(X.shape[0]*X.shape[1]) Y = Y.reshape(Y.shape[0]*Y.shape[1]) |
The next step is, of course, to generate our weights randomly. They need to be rather small, as we would like the input of our sigmoid() function to be sort of close to 0 in the beginning of our training. Do you know why? Think about the back-propagation! This way the gradient of the sigmoid() with respect to its input (i.e., a point close to zero) would be quite high! Think about the slope of the tangent line, on a sigmoid function at a point close to 0. This can make learning faster and accelerate our convergence to a good model! I am not going to dig deeper into it but make sure you understand the concept of back-propagation as it is a crucial one for understanding ANNs and the way they learn!
|
1 2 3 4 |
# We need one random scalar value for W and one for W_0 # We sample from a # uniform distribution between 2 small values around 0, that is the range: [-0.01, 0.01] W = np.random.uniform(low=-0.01, high=0.01, size=(1,)) W_0 = np.random.uniform(low=-0.01, high=0.01, size=(1,)) |
Here comes the exciting part. This is where we will start the training process. Remember:
The learning task in here, means to find the correct weights that would force our sigmoid() function to produce 1’s for all the instances belonging to class 1 and 0’s for the others (class 1 and 0 are just names. You can say negative class and positive class). Remember that the input to the sigmoid() unit is nothing but LITERALLY a simple equation of a line! And the equation is :
and then the sigmoid() function literally squashes this line from both ends to +1 and 0. So, the output of our neural network,
, and is bounded in the range [0, +1].
So, it is clear that it is by the output of the sigmoid(), which happens to be the output of our ANN, that we can decide whether a given x, belongs to class 1 or 0. The training and visualization code is down below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# The number of epochs. This is typical of ANNs to go through the training set many many times # In the beginning of every epoch (i.e., a total sweep through the training set) we usuallu shuffle the data Epoch = 120 # The learning rate! If it is too big, we will jump of the global minimum and might never converge # If it is too small, it might take forever to converge. Needs fine-tuning for every application! eta = 0.001 # This is simply tracking the index of ever sub-plot in the main plot, and will increment as we plot more sub-plots during training subplot_counter = 1 # This list will hold the average cross-entropy error, per epoch. We would like to see it going down! E = [] # This loop counts the epochs for ep in range(Epoch): # Shuffle the train_data X and its Labels Y. The random_index holds the shuffled indices random_index = np.arange(X.shape[0]) np.random.shuffle(random_index) # e will keep track of the cross-entropy in a given epoch for every training data. Then e will be averaged and become an entry in the list E e = [] # Let's go through the random indecis and grab the corresponding X and Y value as for our data and its ground truth (i.e., 0 or 1) for i in random_index: # This is where we compute the Z that is the linear combination of the current data X[i] and the bias weight Z = W*X[i] + W_0 # Here the sigmoid function is applied on Z to compute the output of the network Y_hat = sigmoid(Z) # Compute the Cross Entropy Error and add the error to the list e[]. We call the Cross Entropy Error e.append(Cross_Entropy(Y_hat, Y[i])) # Compute the gradients using the chain-rule and backpropagation. # We call the derivative_Cross_Entropy() and derivative_sigmoid() functions. # The first is the derivative of Error w.r.t. y_hat(i.e., the output), and the # latter is the derivative of y_hat w.r.t z (i.e., the inout to the sigmoid() function) # dEdW is the gradient of Error w.r.t W and dEdW_0 is the gradient of Error w.r.t. W_0 dEdW = derivative_Cross_Entropy(Y_hat, Y[i])*derivative_sigmoid(Y_hat)*X[i] dEdW_0 = derivative_Cross_Entropy(Y_hat, Y[i])*derivative_sigmoid(Y_hat) # Update the parameters using the famous perceptron rule used in backpropagation and gradient descent W = W - eta*dEdW W_0 = W_0 - eta*dEdB # Every 20 times show us how well the line, z, and the sigmoid, y_hat, are doing in separating the samples in class 1 and 0 if ep % 20 == 0: # Plot the training data every time in each subplot and show us the average error at the corresponding epoch plt.title("Epoch Number= %d" % ep + ", Error= %.4f" % np.mean(e)) plt.subplot(2, 3, subplot_counter) plt.scatter(x_0, np.zeros_like(x_0), s=area, c='r', alpha=0.5, label="Class 0") plt.scatter(x_1, np.zeros_like(x_1), s=area, c='c', alpha=0.5, label="Class 1") # In order to have a nice and continuous line, z, we need to get the minimum and maximum of our training data minimum = np.min(X) maximum = np.max(X) # Break all the values between minimum and maximum in steps of 0.01. This gives us enough values to actually plot both z and y_hat s = np.arange(minimum, maximum, 0.01) # Plot the line, z plt.plot(s, W * s + W_0, '-k', label="z") # Plot the sigmoid, y_hat plt.plot(s, sigmoid(W * s + W_0), '+b', label="y_hat") plt.legend() plt.ylim(-0.2, 1.25) plt.grid() # Make sure you increment the subplot index subplot_counter += 1 # Before going to the next epoch, add the average error for the last epoch to E E.append(np.mean(e)) # Create a new figure plt.figure() # Plot E, that is the average binary cross Entropy error per epoch plt.plot(E, c='r') plt.xlabel("Number of Epochs During Training") plt.ylabel("The Binary Cross-Entropy During Training") plt.grid() plt.show() |
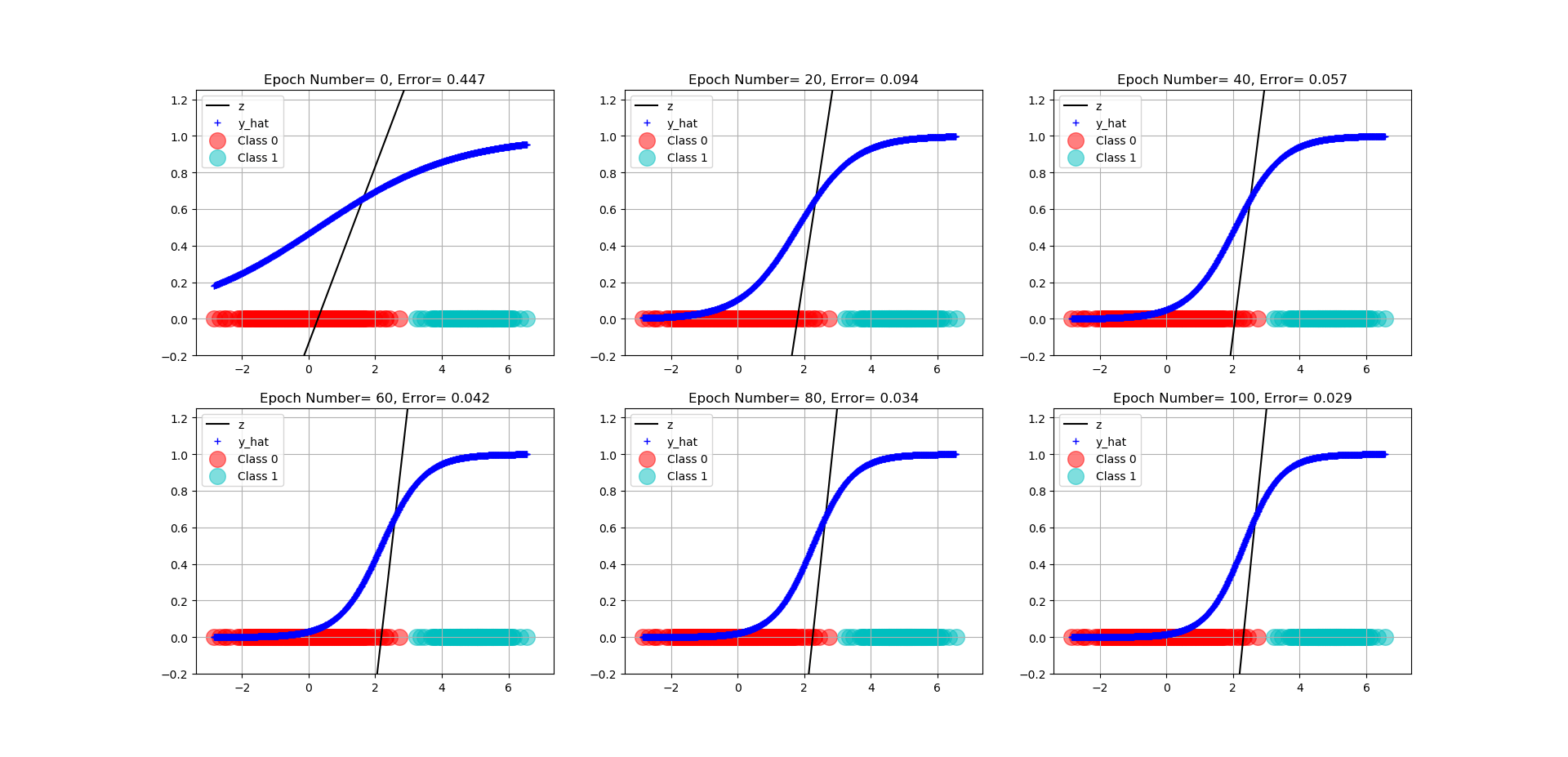
And beautiful enough, of all the 120 epochs that we have trained out network, down below, we can see the progress of the trained model at every 20 epochs. Note how the cross-entropy error is decreasing. Also, note how the black line, that is z, gets squashed and turned into a sigmoidal output whose output is between 0 and 1, that is . You can see how in the very beginning the separation is terrible but then it improves gradually!
And here is the trend of the Error as a function of our training epochs. As you can see, it is pleasantly decreasing!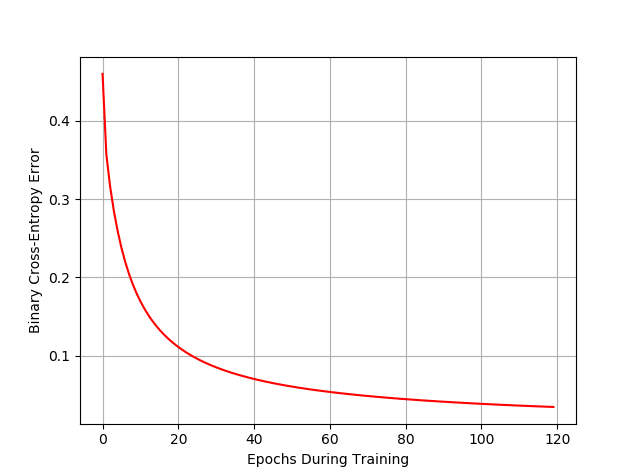
Finally, here is all the code in one place:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import numpy as np<br>import matplotlib.pyplot as plt def Cross_Entropy(y_hat, y): if y == 1: return -np.log(y_hat) else: return -np.log(1 - y_hat) def sigmoid(z): return 1 / (1 + np.exp(-z)) def derivative_Cross_Entropy(y_hat, y): if y == 1: return -1/y_hat else: return 1 / (1 - y_hat) def derivative_sigmoid(x): return x*(1-x) area = 200 N = 500 mu, sigma = 0, 1 # mean and standard deviation x_0 = np.random.normal(mu, sigma, N) x_1 = np.random.normal(mu + 5, sigma*0.50, N) <br>X = [x_0, x_1] Y = [np.zeros_like(x_0), np.ones_like(x_1)] X = np.array(X) Y = np.array(Y) X = X.reshape(X.shape[0]*X.shape[1]) Y = Y.reshape(Y.shape[0]*Y.shape[1]) <br># Define the weights W = np.random.uniform(low=-0.01, high=0.01, size=(1,)) W_0 = np.random.uniform(low=-0.01, high=0.01, size=(1,)) Epoch = 120 eta = 0.001 # Start training subplot_counter = 1 E = [] for ep in range(Epoch): # Shuffle the train_data X and its Labels Y random_index = np.arange(X.shape[0]) np.random.shuffle(random_index) e = [] for i in random_index: Z = W*X[i] + W_0 Y_hat = sigmoid(Z) # Compute the Error e.append(Cross_Entropy(Y_hat, Y[i])) # Compute gradients dEdW = derivative_Cross_Entropy(Y_hat, Y[i])*derivative_sigmoid(Y_hat)*X[i] dEdW_0 = derivative_Cross_Entropy(Y_hat, Y[i])*derivative_sigmoid(Y_hat) # Update the parameter W = W - eta*dEdW W_0 = W_0 - eta*dEdW_0 if ep % 20 == 0: plt.subplot(2, 3, subplot_counter) plt.scatter(x_0, np.zeros_like(x_0), s=area, c='r', alpha=0.5, label="Class 0") plt.scatter(x_1, np.zeros_like(x_1), s=area, c='c', alpha=0.5, label="Class 1") minimum = np.min(X) maximum = np.max(X) s = np.arange(minimum, maximum, 0.01) plt.plot(s, W * s + W_0, '-k', label="z") plt.plot(s, sigmoid(W * s + W_0), '+b', label="y_hat") plt.legend() plt.ylim(-0.2, 1.25) plt.grid() plt.title("Epoch Number= %d" % ep + ", Error= %.3f" % np.mean(e)) subplot_counter += 1 E.append(np.mean(e)) plt.figure() plt.grid() plt.xlabel("Epochs During Training") plt.ylabel("Binary Cross-Entropy Error") plt.plot(E, c='r') plt.show() |