Welcome to MLDawn
Welcome to MLDawn
Welcome to
MLDawn



Recent Posts
At MLDawn we have exciting blog posts on a variety of Machine Learning topics. From the most daunting mathematical concepts to the most exciting coding experience!



An Interview with Prof. Karl Friston
Karl Friston is a theoretical neuroscientist and authority on brain imaging. He invented statistical parametric mapping (SPM), voxel-based morphometry (VBM) and dynamic causal modelling (DCM).

A Gentle 101 Talk on Artificial Neural Networks
What is this post about? In this super gentle 101 talk given at the Insight Centre for Data Analytics at University College Dublin , I
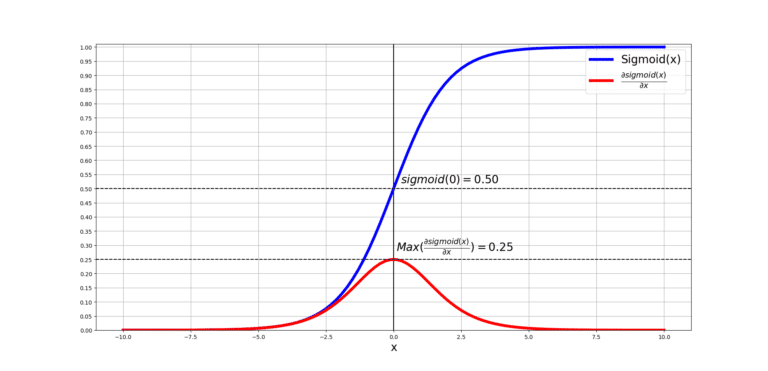
The Backpropagation Algorithm-PART(1): MLP and Sigmoid
What is this post about? The training process of deep Artificial Neural Networks (ANNs) is based on the backpropagation algorithm. Starting with this post, and
Recent Interviews/Talks
MLDawn has a collection of interviews with the giants, as well as exciting presentations and casual talks on Machine Learning!

An Interview with Prof. Karl Friston
Karl Friston is a theoretical neuroscientist and authority on brain imaging. He invented statistical parametric mapping (SPM), voxel-based morphometry (VBM) and dynamic causal modelling (DCM).

A Gentle 101 Talk on Artificial Neural Networks
What is this post about? In this super gentle 101 talk given at the Insight Centre for Data Analytics at University College Dublin , I

An interview with Prof. Mikhail Belkin
We never Had Truly Understood the Bias-Variance Trade-off!!! In this interview with Prof. Mikhail Belkin, we will discuss his amazing paper: “Reconciling modern machine learning


